Bitcoin - митове и легенди (част 2)
Забележка:
Математическите формули в този текст са изписани на LaTeX, за визуализация на който се използва MathJax. Ако вместо формули виждате нещо като\(\Var[nonce] = \frac{1}{p^2}\), то MathJax не функционира по някаква причина, най-вероятно блокиран от NoScript.
В част 1 дадох математическата обосновка на несъстоятелността на редица митове и легенди в света на Bitcoin, породени от субективната невъзможност за правилно възприемане на случайните събития като такива. Сега ще покажа, че процесите всъщност се описват с достатъчно добра точност от теорията и че последната не е само математическо бръщолевене.
Сравнение с експерименталните наблюдения
Разглеждаме следната извадка от публичната статистика на басейна deepbit.net, обхващаща няколко дена на постоянна трудност \(D = 1379192\):
| Период | Блокове | Дялове | Средно | Късмет |
|---|---|---|---|---|
| 29.06 | 57 | 80389531 | 1410343 | +2.3% |
| 30.06 | 64 | 79751252 | 1246113 | –9.6% |
| 01.07 | 62 | 83054752 | 1339593 | –2.9% |
| 02.07 | 57 | 85609229 | 1501916 | +8.9% |
| 03.07 | 55 | 86255018 | 1568273 | +13.7% |
| 04.07 | 65 | 89260819 | 1373243 | –0.4% |
| 05.07 | 51 | 98434841 | 1930095 | +39.9% |
| 29.06–06.07 | 411 | 602755442 | 1466558 | +6.3% |
Късметът е дефиниран като относителното отклонение на средното за деня от математическото очакване. Отрицателните стойности означават късмет, а положителните – каръщина. Върху тези данни може да се приложи т.нар. Z-тест:
$$Z = \frac{mean - \mathrm{E}[shares]}{\sigma / \sqrt{N}}\,,$$
където \(mean\) е средното за деня на броя дялове \(N\), а \(\sigma\) е теоретичното стандартно отклонение на геометричното разпределение. 95% от всички случаи на отклонение от математическото очакване следва да попадат в рамките на \(|Z| \leq 1.96\).
| Период | Блокове | СОСС1 | Късмет | Z-мярка |
|---|---|---|---|---|
| 29.06 | 57 | 13.2% | +2.3% | 0.171 |
| 30.06 | 64 | 12.5% | –9.6% | –0.772 |
| 01.07 | 62 | 12.7% | –2.9% | –0.226 |
| 02.07 | 57 | 13.2% | +8.9% | 0.672 |
| 03.07 | 55 | 13.5% | +13.7% | 1.017 (!) |
| 04.07 | 65 | 12.4% | –0.4% | –0.035 |
| 05.07 | 51 | 14.0% | +39.9% | 2.853 (!!) |
| 29.06–06.07 | 411 | 4.9% | +6.3% | 1.284 (!) |
С (!) е маркирано попадение в горната част на 95% доверителен интервал (\(1 < |Z| \leq 1.96\)). Средната стойност за 05.07 лежи извън рамките на две стандартни отклонения, но попада в рамките на три стандартни отклонения (\(|Z| \leq 3\)), което вече покрива 99.74% от възможните случаи.
Появата на отстоящи далеч от математическото очакване стойности, като например средното за 05.07 е напълно в реда на очакванията, тъй като геометричното разпределение е силно асиметрично, а и централната гранична теорема е приложима за осредняване върху големи извадки. Важно е също така наблюдението, че едно сериозно отклонение на среднодневния брой дялове от математическото очакване може силно да повлияе на средноседмичната стойност.
Съвпадението между теоретичното геометрично разпределение и експерименталното такова е видимо и на следната графика:
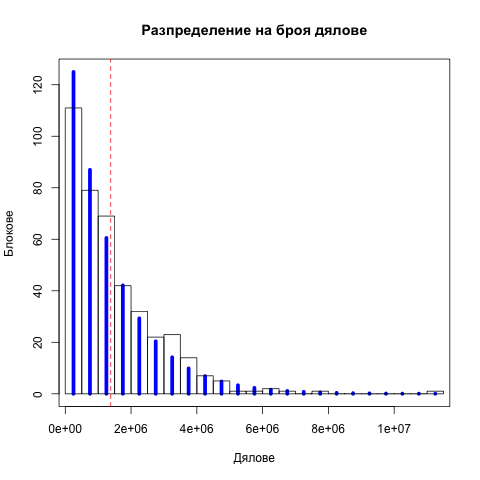
С черно е показана хистограмата на броя блокове като функция на броя дялове за откриването им, а със сините импулси – хистограма на геометричното разпределение. Съвпадението е повече от добро. Вертикалната пунктирана червена линия показва математическото очакване.
В предишната част беше показано, че верояността за срещане на каръшки блок (с повече от средното дялове), последван от два късметлийски блока (с по-малко от средното дялове) е 14.7%, а вероятността за срещане на трите блока в произволен ред е 44.1%. Изброяването на срещането на такъв тип блокове в информацията от deepbit показва, че от общо 409 тройки 58 удовлетворяват шаблона ULL, а 172 тройки удовлетворяват шаблона 1U + 2L, което дава експериментални вероятности:
- \(p_\textrm{exp}(ULL) = \frac{58}{409} = 14.2\%\) при теоретична стойност 14.7%;
- \(p_\textrm{exp}(1U + 2L) = \frac{172}{409} = 42.1\%\) при теоретична стойност 44.1%.
Аналогично, шаблонът ULLL се среща 39 пъти от общо 408 четворки блокове, а шаблонът 1U + 3L – 147 пъти, което дава експериментални вероятности:
- \(p_\textrm{exp}(ULLL) = \frac{39}{408} = 9.6\%\) при теоретична стойност 9.3%;
- \(p_\textrm{exp}(1U + 3L) = \frac{147}{408} = 36.0\%\) при теоретична стойност 37.2%.
Вижда се, че експерименталните стойности са доста близки до теоретичните.
По-строгата дефиниция на късметлийски (по-малко от 1/3 от математичното очакване брой дялове) и каръшки (повече от 3 пъти математичното очакване брой дялове) блокове понижава теоретичните вероятности до \(p(ULL) = 0.4\%\), \(p(1U + 2L) = 1.2\%\), \(p(ULLL) = 0.11\%\) и \(p(1U + 3L) = 0.45\%\). Броят на извадките е твърде малък за надежно наблюдаване на толкова редки събития, което се потвърждава от факта, че комбинацията ULL не се среща нито веднъж, докато комбинацията 1U + 2L се среща само един път. Последното показва колко неправилно е разглеждането на поредицата от блокове само и единствено след срещането на особено каръшки блок.
.. В следващата част ще разгледам процеса на информирано прескачане от басейн на басейн и защо басейните правят всичко възможно да му противодействат.
СОСС – стандартно отклонение на средната стойност ↩︎